задания не открываются

Кинематика 10 класс Задание №4

Мистер Джонс

Задача№1.

За какое время, двигаясь из состояния покоя, Мистер пройдёт путь от дома до ёлки, если он двигается с ускорением  2м/с²?

По графику видно, что путь от дома до ёлки составляет 16 метров

Дано:

S_x=16m

V_x0=0m/s

 a_x=2 м\s²

  t-?

Решение:

V_x0=0m/s,  то S_x= a_xt²/2

t²=2S_x/a_x

t²=2*16m/2m/s²

t²=16s²

t=4s

Задача№2.

Найти скорость Мистера через 5 с по данному уравнению:

V_x=15+2t, построить график зависимости ускорения от времени

Решение:

V_x= V_x0+at

V_x0=15m/s

a_x=2m/s² , отсюда скорость Мистера

V_x=15+5*2=25m/s

Построим график зависимости от времени:

Задача№3.

Какой была начальная скорость Мистера, если через 20с, двигаясь с ускорением 0,5м/с², он достиг скорости  10м/с?

Дано:

V_x=10m/s

a_x=0.5m/s²

t=20s

V_x0 -?

Решение:

V_x= V_x0+at

V_x0= V_x-at

V_x0=10m/s-0.5m/s²*20s

V_x0=0m/s

Кинематика 10 класс Задание №3. (2)

Мистер Джонс.

Задача №4.

По данным графика определить :

•  Начальную координату мистера
•  Проекцию скорости его движения
•  Написать уравнение движения Мистера x=x(t)

Решение:

x₀=5

V_x=(x- x₀)/t

V_x=(-10-5)/3

V_x=5

x= x₀+ V_xt

x=5+5t

Кинематика 10 класс Задание №3.

Mr.Jones

Задача №1.

По дороге движутся равномерно (в одинаковых направлениях) Мистер Джонс и машина. В начальный момент времени координаты Мистера и машины соответственно равны 0м и и -9м, а скорости движения 5м/с и 25м/с соответственно.

• написать уравнения движения Мистера и машины
• определить в какой момент времени и где произойдёт их встреча

Мистер:                                                       Машина:

х=х₀+V_xt                                                       х=х₀+V_xt

х₀=0                                                              х₀=-9

V_x=5                                                             V_x=25

x=5t                                                              x=-9+25t

Встреча:

x₁=x₂   

5t=-9+25t

-20t=-9

t= 0.45

Место:

x=5t

x=5*0.45

x=2.25

Задача №2.

На рисунке показан Мистер Джонс.

• описать характер движения Мистера по данным рисунка
• составить уравнение движения Мистера при равномерном движении
• найти в какой момент времени Мистер дойдёт до ёлки, если её координата равна -8

Мистер:

х=х₀+V_xt                                                      

х₀=0

V_x=10

х=10t

Встреча:

Так как координата ёлки -8, то составим уравнение:

-8=10t

t=-0.8

 Задача №3.

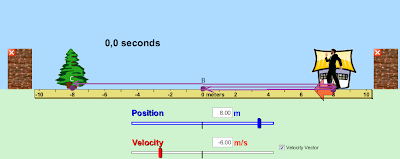
Мистер Джонс вышел из дома по направлению к ёлке. В начале координат он вспомнил, что забыл что-то дома и вернулся обратно, затем продолжил свой путь к ёлке. Всё время Мистер двигался с постоянной скоростью 6м/с. 

• определить путь, пройденный Мистером до ёлки
• определить время, потраченное Мистером в пути до ёлки

По графику видно, что начальная координата Мистера равна 8, а координата ёлки равна -8

Путь:

l= АВ+ВА+АС

l= 8m+8m+16m

l=32m

Так как Мистер шёл с постоянной скоростью 6м/с, то

t=32*6

t=192s

t=3min12s

Кинематика 10 класс, задание №2.

Определение проекции вектора на ось

Вариант №1

Цель:

• определить координаты начала и конца вектора
• определить проекции векторов на ось
• определить длину векторов
• определить сумму и разность двух предложенных векторов

1)

Вектор АВ:

Начальные координаты                                     Конечные координаты

x₀=3                                                                      x=7

y₀=2                                                                      y=8

Проекции векторов:

 Sx=x-x₀                                            Sy=y-y₀

 Sx=7-3=4                                      Sy=8-2=6

Длина вектора АВ:

S²=Sx²+Sy²           S=16+36=52

S≈7.2

Вектор СD:

Начальные координаты                                     Конечные координаты

x₀=8                                                                        x=14

y₀=4                                                                        y=6

Проекции векторов:

Sx=x-x₀                                            Sy=y-y₀

 Sx=14-8=6                                   Sy=6-4=2

Длина вектора CD:

S²=Sx²+Sy²           S=36+4=40

S≈6.3

2) Сумма AB+CD

Переместим векторы так, чтобы начальная точка CD лежала в конечной точке AB

AB+CD=AD

A  x₀=3                                                                  D  x=13

     y₀=2                                                                       y=10

Проекции векторов:

Sx=x-x₀                                            Sy=y-y₀

Sx=13-3=10                                  Sy=10-2=8

Длина вектора AD:

S²=Sx²+Sy²           S=100+64=164

S≈12.8

3) Разность AB-CD

Переместим векторы так, чтобы оба вектора AB и CD выходили из одной точки

AB-CD=BD

B  x₀=7                                                                  D  x=9

     y₀=8                                                                      y=4

Проекции векторов:

Sx=x-x₀                                            Sy=y-y₀

Sx=9-7=2                                      Sy=4-8=-4

Длина вектора BD:

S²=Sx²+Sy²         S=4+16=20

S≈4.4

Кинематика 10 класс Задание №1

Определение перемещения Божьей Коровки

Цель работы:

·       1, определить проекции перемещения и величины самого перемещение БК

·      2,  сравнить путь и перемещение БК  
    1)  

  

 вРезультаты измерений:

Вектор АВ

Начальные координаты                                     Конечные координаты

x₀=13                                                                    x=15

y₀=3                                                                      y=11

Проекции векторов:

 Sx=x-x₀                                            Sy=y-y₀

 Sx=15-13=2                                      Sy=11-3=8

Длина вектора АВ:

S²=Sx²+Sy²       S²=4+64=68

S≈8.2

Сравним путь и перемещение:

По графику видно, что путь и перемещение не равны. Путь больше перемещения.

2)  

Результаты измерений:

Вектор АВ

Начальные координаты                                     Конечные координаты

x₀=-8                                                                     x=7

y₀=5                                                                      y=2

Проекции векторов:

 Sx=x-x₀                                            Sy=y-y₀

 Sx=7-(-8)=15                             Sy=2-5=-3

Длина вектора АВ:

S²=Sx²+Sy²       S²=255+9=264

S≈16.2

Сравним путь и перемещение:

По графику видно, что путь и перемещение не равны. Путь больше перемещения.

 3) 

Результаты измерений:

Вектор АВ

Начальные координаты                                     Конечные координаты

x₀=1                                                                      x=11

y₀=4                                                                      y=-8

Проекции векторов:

 Sx=x-x₀                                            Sy=y-y₀

 Sx=11-1=10                                  Sy=-8-4=-12

Длина вектора АВ:

S²=Sx²+Sy²       S²=100+144=244

S≈15.6

Сравним путь и перемещение:

По графику видно, что путь и перемещение не равны. Путь больше перемещения.